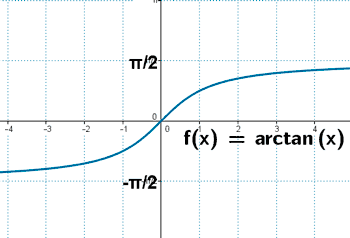Funciones
Una función matemática es la correspondencia o relación f de los elementos de un conjunto A con los elementos de un conjunto B. Una función cumple con la condición de existencia (todos los elementos de A están relacionados con los elementos de B) y con la condición de unicidad (cada elemento de A está relacionado con un único elemento de B).
Tipos de funciones
Función polinómica


El dominio de las funciones polinómicas son todos los números reales.
Las funciones polinómicas son continuas en todo su dominio.
ejemplo

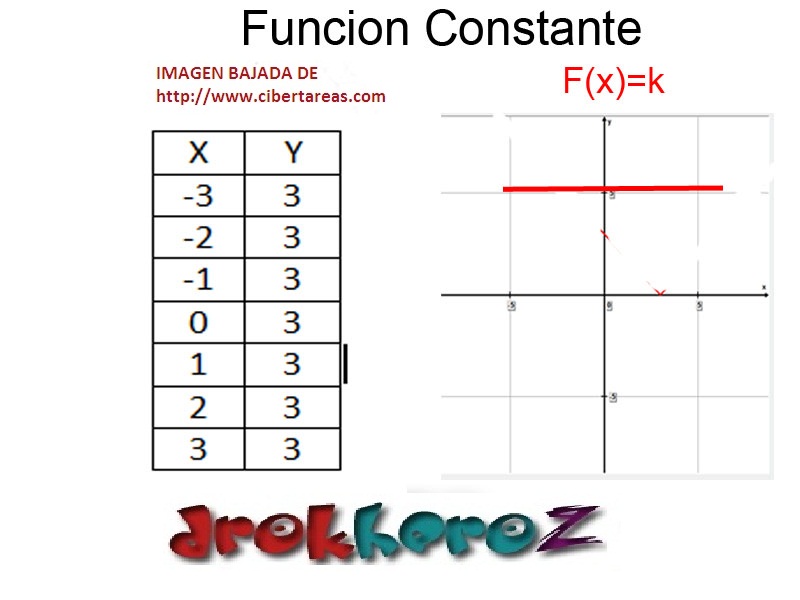
Función Constante
Una función f es constante si la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x).


En términos matemáticos, la función f es constante si para cualquier par de puntos x1 y x2 del dominio tales que x1<x2, se cumple que f(x1) = f(x2).
Ejemplo
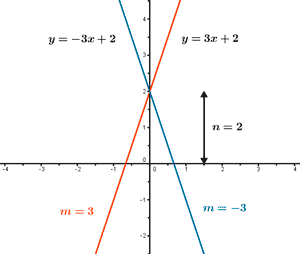
Función polinómica de primer grado
Las funciones polinómicas de primer grado o de grado 1 son aquellas que tienen un polinomio de grado 1 como expresión. Están compuestas por un escalar que multiplica a la variable independiente más una constante. Su mayor exponente es x elevado a 1.


Su representación gráfica es una recta de pendiente m.
Ejemplo
Funcíon afín
Una función afín es una función polinómica de primer grado que no pasa por el origen de coordenadas, o sea, por el punto (0,0).
Las funciones afines son rectas definidas por la siguiente fórmula:


Ejemplo

Función Lineal
Una función lineal es una función polinómica de grado 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Son funciones rectas de la forma:


Ejemplo

Función identidad
Una función identidad es una función tal que la imagen de cualquier elemento es éste mismo:


Ejemplo

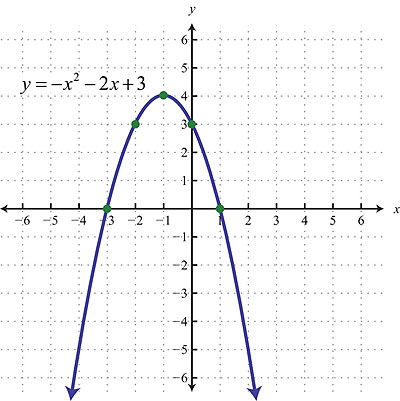
Función cuadrática
Las funciones cuadráticas (o funciones de segundo grado) son funciones polinómicas de grado 2, es decir, el mayor exponente del polinomio es x elevado a 2 (x2):



Ejemplo
Función cúbica
Las funciones cúbicas (o funciones de tercer grado) son funciones polinómicas de grado 3, es decir, las que el mayor exponente del polinomio es x elevado a 3 (x3):



Ejemplo

Función racional
Las funciones racionales f(x) son el cociente de dos polinomios. La palabra racional hace referencia a que esta función es una razón.



Ejemplo

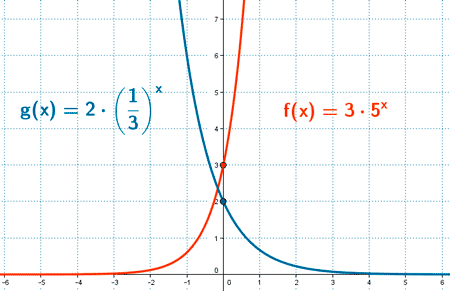
Función exponencial
Una función exponencial es aquella que la variable independiente x aparece en el exponente y tiene de base una constante a. Su expresión es:



Ejemplo
Función logarítmica
Una función logarítmica está formada por un logaritmo de base a, y es de la forma:



Ejemplo

Funciones definidas a trozos
Las funciones definidas a trozos (o función por partes) si la función tiene distintas expresiones o fórmulas dependiendo del intervalo (o trozo) en el que se encuentra la variable independiente (x).

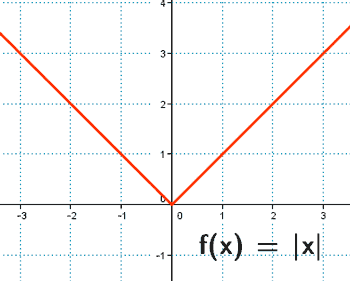


Ejemplo
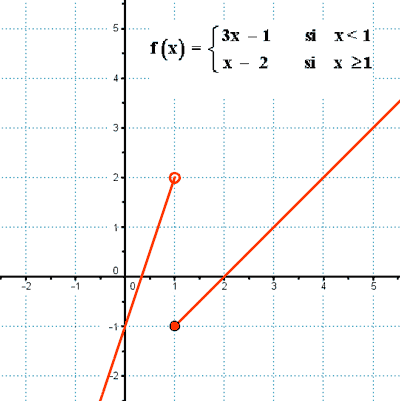
Funciones trigonométricas
Seno

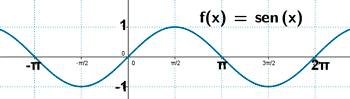
Ejemplo
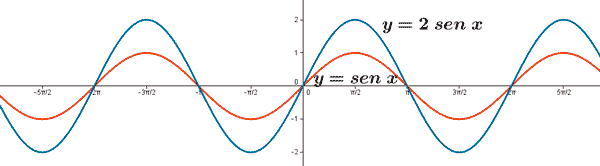
Coseno

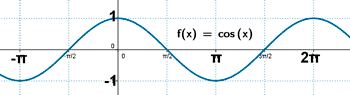
Ejemplo

Tangente

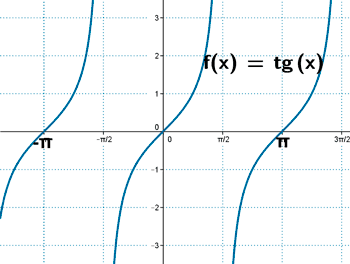
Ejemplo
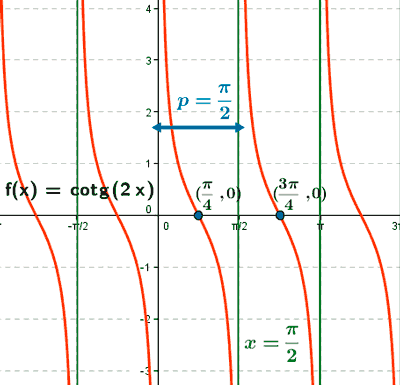
Cotangente

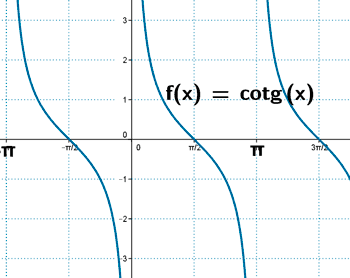
Ejemplo
Secante

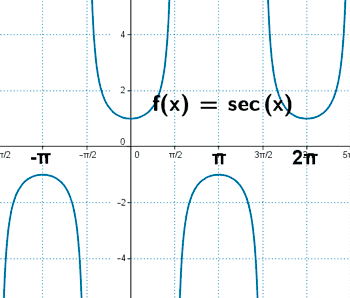
Cosecante

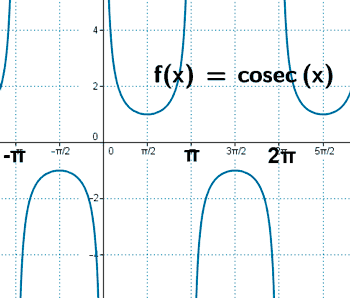
Arcoseno

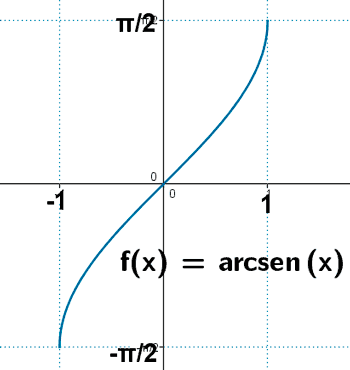
Arcocoseno

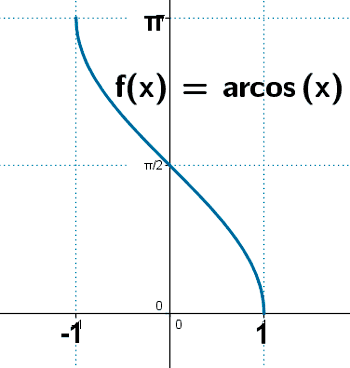
Arcotangente