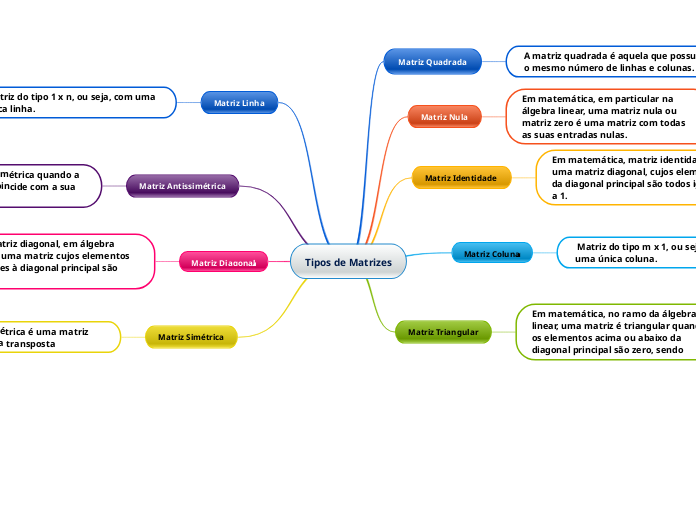
Tipos de Matrizes

Matriz Quadrada

A matriz quadrada é aquela que possui o mesmo número de linhas e colunas.

Matriz Nula

Em matemática, em particular na álgebra linear, uma matriz nula ou matriz zero é uma matriz com todas as suas entradas nulas.

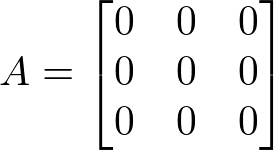
Matriz Identidade

Em matemática, matriz identidade é uma matriz diagonal, cujos elementos da diagonal principal são todos iguais a 1.

Matriz Coluna^

Matriz do tipo m x 1, ou seja, com uma única coluna.

Matriz Triangular

Em matemática, no ramo da álgebra linear, uma matriz é triangular quando os elementos acima ou abaixo da diagonal principal são zero, sendo chamada matriz triangular inferior e matriz triangular superior, respectivamente.^

Matriz Linha

Matriz do tipo 1 x n, ou seja, com uma única linha.

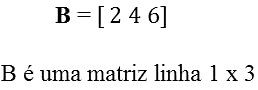
Matriz Antissimétrica

Uma matriz é anti-simétrica quando a matriz transposta coincide com a sua matriz oposta

Matriz Diagonal^

Uma matriz diagonal, em álgebra linear, é uma matriz cujos elementos exteriores à diagonal principal são nulos.

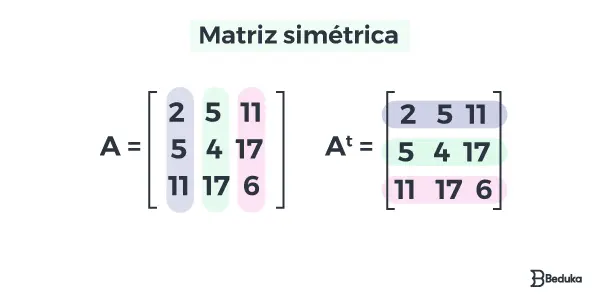
Matriz Simétrica

Uma matriz simétrica é uma matriz que é igual à sua transposta

Operações com Matrizes

Matriz Inversa

Seja A uma matriz quadrada, sua inversa A^-1, onde A*A^-1 = I

Multiplicação por escalar

Quando trabalhamos matrizes, chamamos os números reais de escalares. O termo multiplicação escalar refere-se ao produto de um número real com uma matriz. Em multiplicações escalares, cada elemento da matriz é multiplicado pelo escalar determinado.

Matriz Adjunta

Em álgebra linear uma matriz adjunta de uma matriz quadrada é a transposta de sua matriz dos cofatores.

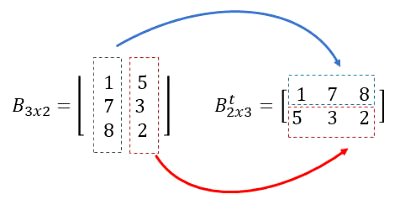
Matriz Transposta

Em matemática, matriz transposta é a matriz que se obtém da troca de linhas por colunas de uma dada matriz.

Adição e Subtração

Dadas duas matrizes de mesmo tipo, A e B, denomina-se matriz soma (A+B) a matriz obtida adicionando-se os elementos correspondentes de A e B. Da mesma forma, a matriz (A-B) é obtida subtraindo os elementos correspondentes.

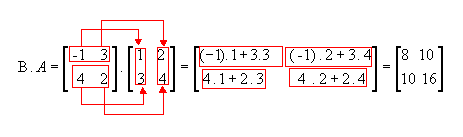
Multiplicação por matrizes

Para ser possível multiplicar matrizes, é primordial que o número de colunas da primeira matriz seja igual ao número de linhas da segunda matriz.

Igualdade de matrizes

Devem ter a mesma ordem, ou seja, o mesmo número de linhas e o mesmo número de colunas. Os elementos devem ser iguais aos seus correspondentes.

Determinantes

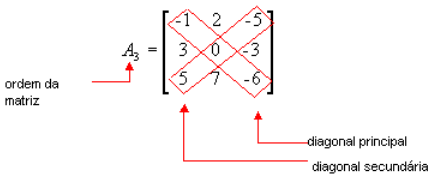
Segunda Ordem

O determinante de uma matriz de segunda ordem é a diferença entre o produto dos termos da diagonal principal e o produto dos termos da diagonal secundária.

Terceira Ordem

Para calcular o determinante desse tipo de matriz, utilizamos a Regra de Sarrus.

Teorema de Laplace

O teorema de Laplace, assim como a regra de Sarrus, é um método para encontrar o determinante de uma matriz. Enunciado do teorema: Seja A uma matriz quadrada, o determinante de A, ou seja, det (A), é igual à soma dos produtos dos elementos de uma fila (linha ou coluna) pelos seus respectivos cofatores.

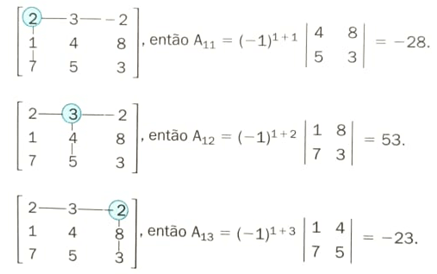
Cofatores

O cofator de uma matriz de ordem n ≥ 2 é definido como:

Aij = (-1) i + j. Dij